Le curve via via generate qui sotto stanno in un piccolo spazio.
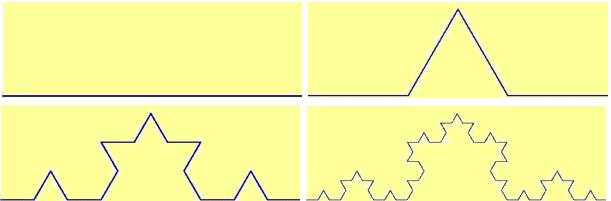
La loro lunghezza a che valore tende?

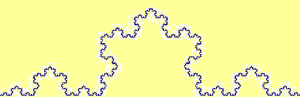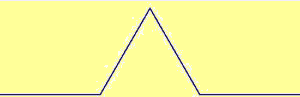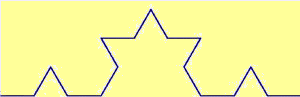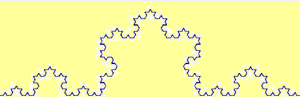Sul terzo centrale di un segmento lungo 1 viene costruito un triangolo equilatero e viene cancellato il lato che sta sul segmento iniziale. E così via sui nuovi lati. La lunghezza della curva via via costruita quale valore tende ad assumere?

Il segmento iniziale è lungo 1. La successiva curva è ottenuta sostituendo un terzo di segmento con due segmenti altrettanto lunghi: è lunga 1+1/3 = 4/3 = 1.333…. La successiva curva è ottenuta operando la stessa sostituzione sui 4 segmenti precedenti, che diventano ciascuno lungo 1/3*4/3, avendo una curva lunga in tutto 4/3*4/3 = 1.777…. La successiva curva è ottenuta operando la stessa sostituzione sui nuovi 16 segmenti, avendo una curva lunga in tutto 4/3*4/3*4/3 = (4/3)^3 = 2.370370370...
La lunghezza dopo N trasformazioni è (4/3)^N, valore che al crescere di N tende all'infinito!
È una curva la cui lunghezza cresce oltre ogni limitazione in uno spazio limitato!

Figure generate in modo simile a quelli descritti in questo documento e nei due precedenti  (uno  e  due)  sono chiamate frattali.
Un frattale è una figura geometrica che è la configurazione limite di una successione di figure ottenute una dall'altra mediante una regola assegnata e che ha l'aspetto di una immagine in cui si ripete all'infinito, con grandezza via via più piccola, una stessa forma.  Il nome deriva dal fatto che, data una opportuna definizione di dimensione, a una figura di questo tipo viene assegnata una dimensione frazionaria.  La teoria dei frattali è stata elaborata da B. B. Mandelbrot nel 1975, e può essere utilizzata per descrivere figure complesse della realtà.